Asallar: Sayılar Dünyasının Cazibesi ve Gelecekteki Maceramız Asal sayılar, tarihin en başlarından beri matematikçilerin ve sayı severlerin ilgisini üzerine çeken gizemli varlıklar olmuştur. Her biri yalnızca kendine ve bire bölünebilen bu özel sayılar, yüzyıllardır araştırmacıların zihinlerini meşgul etti. Peki, asal sayılara olan bu tutkumuz nereden geliyor ve onları bulma çabalarımız nereye doğru evriliyor? Gelin, bu sonsuz serüvene birlikte dalalım ve geleceğin heyecanlandırıcı keşiflerine göz atalım.

Yaklaşık 20,000 yıl öncesine ait, üzerinde düzensiz işaretler bulunan pürüzsüz bir kemik parçası arkeologları şaşırttı, ta ki bu işaretlerde bir farklılık keşfedene kadar – işaretler, çentikler gibi görünen bu çizgiler asal sayıları temsil ediyor olabilir. Benzer şekilde, Babil rakamlarıyla yazılmış M.Ö. 1800 tarihli bir kil tablet, asal sayılara dayalı bir sayı sistemini tarif ediyor.

Tarihte yer alan Ishango kemiği, Plimpton 322 tableti ve diğer eserlerin gösterdiği gibi, asal sayılar her zaman insanların ilgisini çekmiş ve dikkatini çekmiştir. Günümüzde, asal sayılar ve özellikleri sayı teorisi altında, matematikte önemli bir araştırma konusu olarak incelenmektedir.

Asal Sayıların Tarihi

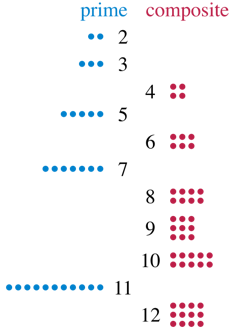
Gayri resmi olarak, birden büyük pozitif bir sayı, eğer yalnızca bir sütun veya bir sıra ile düzenlenebilirse asaldır. Örneğin, 11 bir asal sayıdır çünkü 11 nokta sadece 1’e 11 ve 11’e 1 boyutunda dikdörtgen düzenlemeler oluşturur. Tersine, 12 asal sayı değildir çünkü 12 noktayı 3’e 4’lük bir dizi yapmakta kullanabilirsiniz, bu da birden fazla sıra ve sütun içerir. Matematik kitapları asal sayıyı, birden büyük ve yalnızca kendine ve 1’e bölünebilen bir tam sayı olarak tanımlar.

Matematik tarihçisi Peter S. Rudman Yunan matematikçilerinin yaklaşık M.Ö. 500 yıllarında asal sayı kavramını anlayan ilk kişiler olduğunu önerir.

M.Ö. 300 civarında, Yunan matematikçi ve mantıkçı Euler sonsuz sayıda asal sayı olduğunu kanıtladı. Euler, başlangıçta sonlu sayıda asal sayı olduğunu varsayarak başlayıp, ardından orijinal listede olmayan bir asal sayı bularak bir çelişki yarattı. Matematiğin temel bir ilkesi, çelişki olmadan mantıksal tutarlılıktır, dolayısıyla Euler başlangıç varsayımının yanlış olduğunu sonuçlandırdı. Böylece, sonsuz sayıda asal sayı var.

Bu argüman sonsuz asal sayıların varlığını kanıtladı, ancak özellikle verimli değildi. Euler tüm asal sayıları artan şekilde listelemek için etkin bir yöntem geliştiremedi.

Orta Çağ’da, Arap matematikçiler, hasam sayıları olarak bilinen asal sayıların teorisini geliştirdiler. Pers matematikçi Kamal al-Din al-Farisi, asal sayıların temel aritmetik teoremini formüle etti. Bu, birden büyük herhangi bir pozitif tamsayının mutlaka asal sayıların çarpımı olarak ifade edilebileceğini belirtir.

Bu görüşe göre, asal sayılar herhangi bir pozitif tam sayıyı çarparak yapmak için temel yapı taşlarıdır – kimyada atomların molekül oluşturması gibi.

Asal sayılar farklı tiplere ayrılabilir. 1202’de, Leonardo Fibonacci “Liber Abaci: Hesaplama Kitabı” adlı kitabında p’nin de asal olması durumunda (2^p – 1) biçimindeki asal sayıları tanıttı.

Günümüzde, bu formattaki asal sayılar, Fransız rahip Marin Mersenne‘den sonra Mersenne asal sayıları olarak adlandırılır. Bilinen en büyük asal sayıların çoğu bu formattadır.

Birçok erken matematikçi, p asal ise, (2^p – 1) biçimindeki bir sayının asallar olduğuna inanıyordu. Ancak 1536’da, matematikçi Hudalricus Regius fark etti ki 11 asal, ancak (2¹¹ – 1) 2047 olduğu için asal değildir. Bu sayı 11 x 89 olarak ifade edilebilir ve bu doğru değildir.

Her zaman doğru olmasa da, sayı teorisyenler (2^p – 1) kısayolunun sıklıkla asal oluşturduğunu ve büyük asal aramaları için sistematik bir yol sunduğunu fark ettiler.

Büyük Asalların Peşinde

(2^p – 1) sayısı p’nin değerine göre oldukça büyük olur ve büyük asalları belirleme fırsatları sunar.

Ancak (2^p – 1) sayısı yeterince büyük olduğunda, (2^p – 1) asal olup olmadığını kontrol etmek çok daha zor hale gelir – yani (2^p – 1) noktaların sadece bir sütun veya bir sıra ile dikdörtgen bir düzenleme oluşturup oluşturamayacağını kontrol etmek zordur.

Neyse ki, Édouard Lucas 1878’de bir asal sayı testi geliştirdi, bu test daha sonra 1930’da Derrick Henry Lehmer tarafından kanıtlandı. Bu çalışma, Mersenne asal sayılarını değerlendirmek için verimli bir algoritma ortaya çıkardı. Lucas, 1876’da, el hesaplamalarıyla kağıt üzerinde, 39 haneli (2¹²⁷ – 1) sayısının 170,141,183,460,469,231,731,687,303,715,884,105,727 olduğunu ve bu değerin asal olduğunu gösterdi.

M127 olarak da bilinen bu sayı, el hesaplamaları yoluyla doğrulanan en büyük asal olarak kayıtlara geçti. 75 yıl boyunca en büyük bilinen asal rekorunu elinde tuttu.

Araştırmacılar, 1950’lerde bilgisayarları kullanmaya başladılar ve yeni büyük asal sayıların keşif hızı arttı. 1952’de, Raphael M. Robinson, Standart Batı Otomatik Bilgisayar kullanarak birkaç yeni Mersenne asal sayısı tanımladı.

Bilgisayarlar gelişmeye devam ettikçe, Mersenne asal listesi büyüdü, özellikle 1964’te Cray süper bilgisayarının gelişiyle. Her ne kadar sonsuz sayıda asal sayı olsa da, araştırmacılar (2^p – 1) türündeki asal sayılar ve Mersenne asal sayıları arasında kaç tane olduğunu belirlemekte zorlanıyorlar.

1980’li yılların başlarına gelindiğinde, araştırmacılar yeterince veri biriktirmişti ve bu da onlara Mersenne asal sayılarının sonsuz sayıda olduğuna inanacak kadar güven verdi. Bu asal sayıların ortalama olarak ne sıklıkta ortaya çıktığını tahmin edebilmişlerdi. Matematikçiler henüz bunu kanıtlamadı ama yeni veriler bu tahminleri sürekli destekliyor.

George Woltman, bir bilgisayar bilimcisi, 1996 yılında Büyük İnternet Mersenne Asal Arama, ya da GIMPS adlı projeyi başlattı. Bu işbirlikçi program aracılığıyla, herkes GIMPS web sitesinden Mersenne asal sayılarını aramak için kişisel bilgisayarlarına ücretsiz yazılım indirebilir. Web sitesi, nasıl katılacağına dair özel talimatlar içeriyor.

GIMPS şimdiye kadar 18 Mersenne asal sayısı tespit etti, bunların çoğu kişisel bilgisayarlarda Intel çipleri kullanarak bulundu. Program ortalama olarak her bir ila iki yılda bir yeni keşif gerçekleştiriyor.

Bilinen En Büyük Asal Sayı

Luke Durant, emekli bir programcı, şu anki en büyük bilinen asal sayıyı, (2^136,279,841 – 1) buldu. Ekim 2024’te, M136279841 olarak anılıyor, bu 41,024,320 haneli sayı 52. Mersenne asal sayısıydı ve halka açık bir bulut tabanlı bilişim ağı üzerinde GIMPS çalıştırarak bulundu.

Bu ağ, Nvidia çipleri kullandı ve 17 ülke ile 24 veri merkezi boyunca çalıştı. Bu gelişmiş çipler çok sayıda hesaplamayı aynı anda ele alarak daha hızlı bilgi işlem sağlar. Sonuç, asal sayı testi gibi algoritmalar için daha kısa çalışma süreleridir.

Elektronik Sınır Vakfı, büyük asal sayıları tespit edenlere para ödülleri sunan bir sivil özgürlük grubudur. 2000 ve 2009’da ödüller, ilk doğrulanmış 1 milyon haneli ve 10 milyon haneli asal sayılar için ödüller verdi.

Büyük asal sayı meraklılarının bir sonraki iki hedefi, ilk 100 milyon haneli ve 1 milyar haneli asal sayıları belirlemek. EFF ödülleri olarak US$150,000 ve $250,000, sırasıyla ilk başarılı birey veya ekibi bekliyor.

Bilinen en büyük 10 asal sayının sekizi Mersenne asalı olduğu için, GIMPS ve bulut bilişim, rekor kıran büyük asal sayıları aramada önemli bir rol oynamaya hazırlanıyor.

Büyük asal sayılar, birçok siber güvenlik şifreleme yönteminde hayati bir rol oynar, bu yüzden her internet kullanıcısı büyük asal sayıların arayışından faydalanır. Bu arayışlar, dijital iletişimi ve hassas bilgileri güvende tutar.

Jeremiah Bartz, Matematik Doçenti, Kuzey Dakota Üniversitesi. Bu makale The Conversation‘dan Creative Commons lisansı altında yeniden yayınlanmıştır. Orijinal makaleyi okuyun.